Introduction of Transformations
Computer Graphics provide the facility of viewing object from different angles. The architect can study building from different angles i.e.
- Front Evaluation
- Side elevation
- Top plan
A Cartographer can change the size of charts and topographical maps. So if graphics images are coded as numbers, the numbers can be stored in memory. These numbers are modified by mathematical operations called as Transformation.
The purpose of using computers for drawing is to provide facility to user to view the object from different angles, enlarging or reducing the scale or shape of object called as Transformation.
- Each transformation is a single entity. It can be denoted by a unique name or symbol.
- It is possible to combine two transformations, after connecting a single transformation is obtained, e.g., A is a transformation for translation. The B transformation performs scaling. The combination of two is C=AB. So C is obtained by concatenation property.
There are two complementary points of view for describing object transformation.
- Geometric Transformation: The object itself is transformed relative to the coordinate system or background. The mathematical statement of this viewpoint is defined by geometric transformations applied to each point of the object.
- Coordinate Transformation: The object is held stationary while the coordinate system is transformed relative to the object. This effect is attained through the application of coordinate transformations.
An example that helps to distinguish these two viewpoints:
The movement of an automobile against a scenic background we can simulate this by
- Moving the automobile while keeping the background fixed-(Geometric Transformation)
- We can keep the car fixed while moving the background scenery- (Coordinate Transformation)
Types of Transformations:
- Translation
- Scaling
- Rotating
- Reflection
- Shearing
Translation
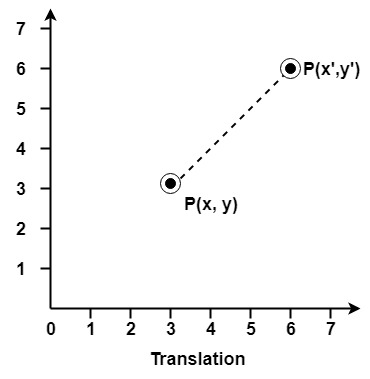
It is the straight line movement of an object from one position to another is called Translation. Here the object is positioned from one coordinate location to another.
Translation of point:
To translate a point from coordinate position (x, y) to another (x1 y1), we add algebraically the translation distances Tx and Ty to original coordinate.
x1=x+Tx
y1=y+Ty
The translation pair (Tx,Ty) is called as shift vector.
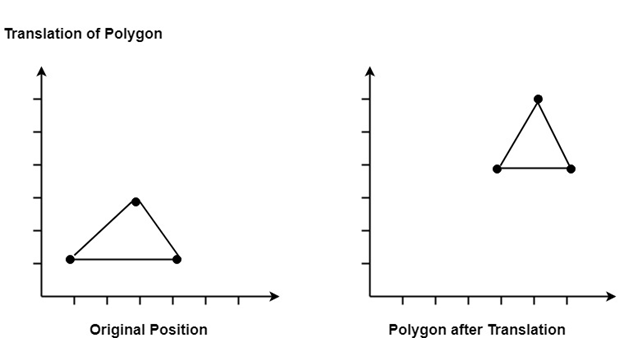
Translation is a movement of objects without deformation. Every position or point is translated by the same amount. When the straight line is translated, then it will be drawn using endpoints.
For translating polygon, each vertex of the polygon is converted to a new position. Similarly, curved objects are translated. To change the position of the circle or ellipse its center coordinates are transformed, then the object is drawn using new coordinates.
Let P is a point with coordinates (x, y). It will be translated as (x1 y1).
Matrix for Translation:
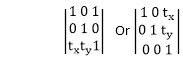
Scaling:
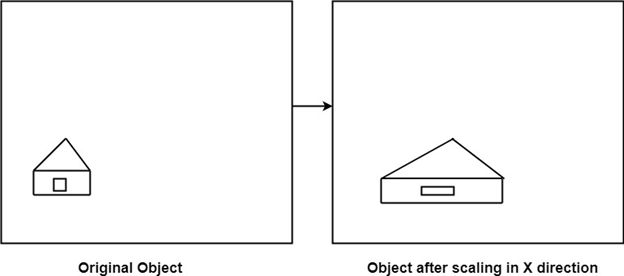
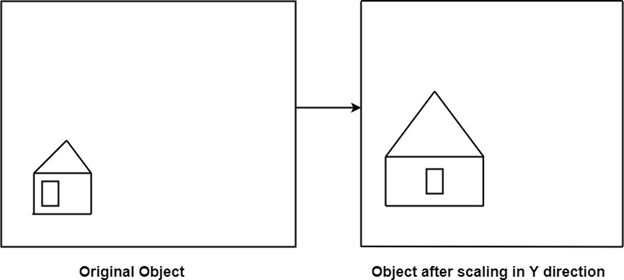
It is used to alter or change the size of objects. The change is done using scaling factors. There are two scaling factors, i.e. Sx in x direction Sy in y-direction. If the original position is x and y. Scaling factors are Sx and Sy then the value of coordinates after scaling will be x1 and y1.
If the picture to be enlarged to twice its original size then Sx = Sy =2. If Sxand Sy are not equal then scaling will occur but it will elongate or distort the picture.
If scaling factors are less than one, then the size of the object will be reduced. If scaling factors are higher than one, then the size of the object will be enlarged.
If Sxand Syare equal it is also called as Uniform Scaling. If not equal then called as Differential Scaling. If scaling factors with values less than one will move the object closer to coordinate origin, while a value higher than one will move coordinate position farther from origin.
Enlargement: If T1=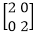 ,If (x1 y1)is original position and T1is translation vector then (x2 y2) are coordinated after scaling
,If (x1 y1)is original position and T1is translation vector then (x2 y2) are coordinated after scaling
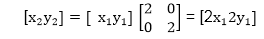
The image will be enlarged two times
Reduction: If T1= . If (x1 y1) is original position and T1 is translation vector, then (x2 y2) are coordinates after scaling
. If (x1 y1) is original position and T1 is translation vector, then (x2 y2) are coordinates after scaling
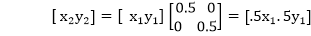
Matrix for Scaling:
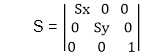
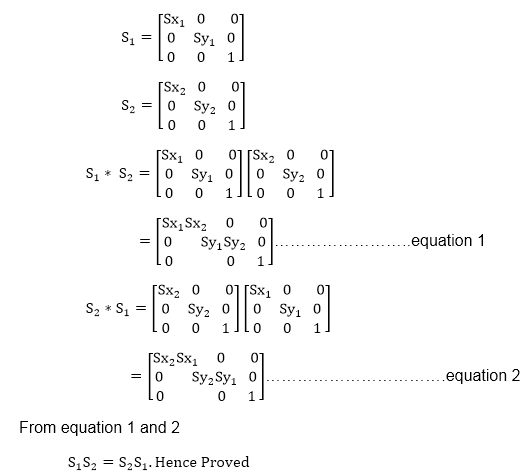
Example: Prove that 2D Scaling transformations are commutative i.e, S1 S2=S2 S1.
Solution: S1 and S2 are scaling matrices
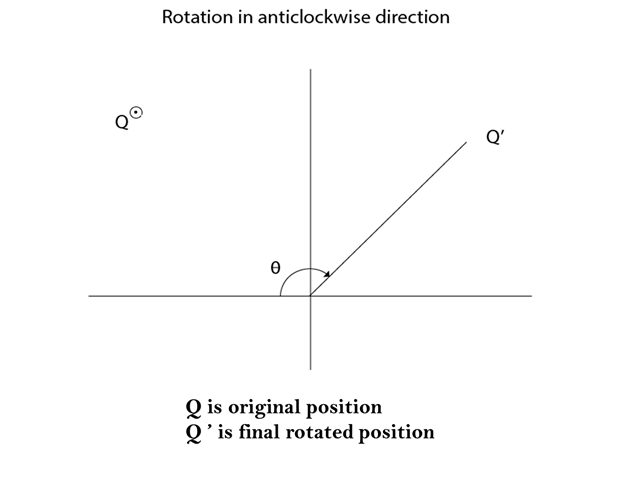
Rotation:
It is a process of changing the angle of the object. Rotation can be clockwise or anticlockwise. For rotation, we have to specify the angle of rotation and rotation point. Rotation point is also called a pivot point. It is print about which object is rotated.
Types of Rotation:
- Anticlockwise
- Counterclockwise
The positive value of the pivot point (rotation angle) rotates an object in a counter-clockwise (anti-clockwise) direction. The negative value of the pivot point (rotation angle) rotates an object in a clockwise direction. When the object is rotated, then every point of the object is rotated by the same angle.
Straight Line: Straight Line is rotated by the endpoints with the same angle and redrawing the line between new endpoints.
Polygon: Polygon is rotated by shifting every vertex using the same rotational angle.
Curved Lines: Curved Lines are rotated by repositioning of all points and drawing of the curve at new positions.
Circle: It can be obtained by center position by the specified angle.
Ellipse: Its rotation can be obtained by rotating major and minor axis of an ellipse by the desired angle.
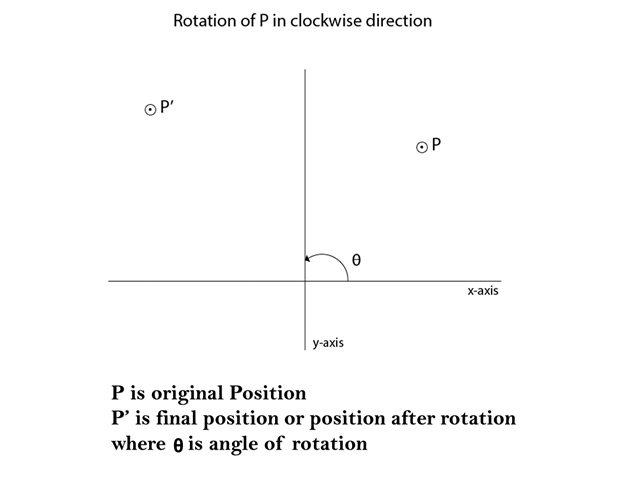
Matrix for rotation is a clockwise direction.

Matrix for rotation is an anticlockwise direction.
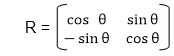
Matrix for homogeneous co-ordinate rotation (clockwise)

Matrix for homogeneous co-ordinate rotation (anticlockwise)
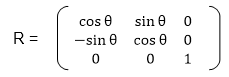
Rotation about an arbitrary point:
If we want to rotate an object or point about an arbitrary point, first of all, we translate the point about which we want to rotate to the origin. Then rotate point or object about the origin, and at the end, we again translate it to the original place. We get rotation about an arbitrary point.
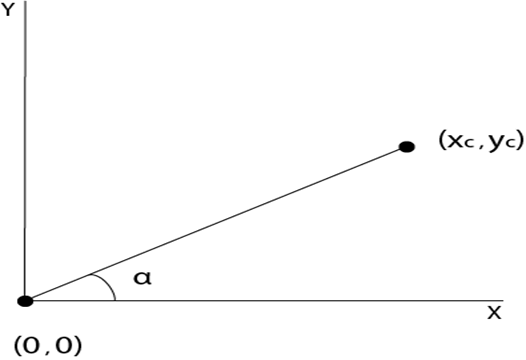
Example: The point (x, y) is to be rotated
The (xc yc) is a point about which counterclockwise rotation is done
Step1: Translate point (xc yc) to origin
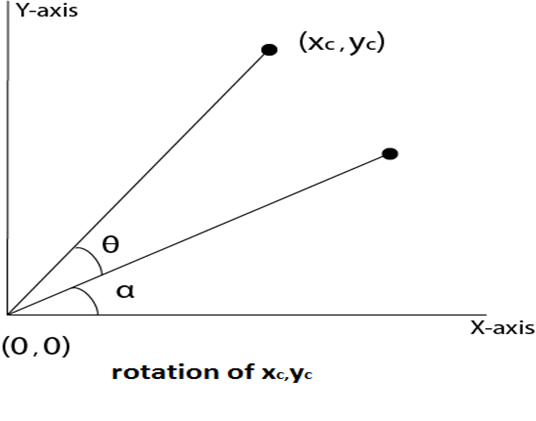
Step2: Rotation of (x, y) about the origin
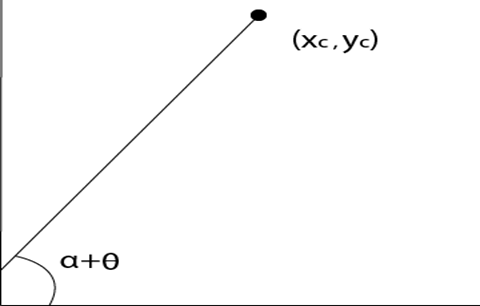
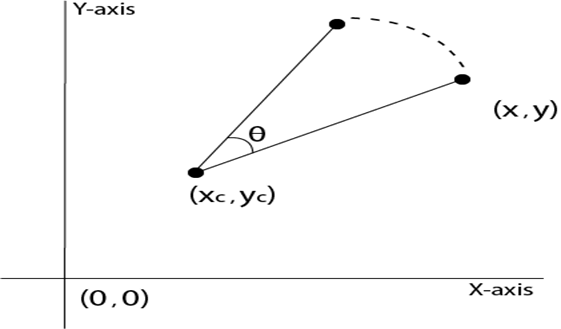
Step3: Translation of center of rotation back to its original position
Example1: Prove that 2D rotations about the origin are commutative i.e. R1 R2=R2 R1.
Solution: R1 and R2are rotation matrices

Reflection:
It is a transformation which produces a mirror image of an object. The mirror image can be either about x-axis or y-axis. The object is rotated by180°.
Types of Reflection:
- Reflection about the x-axis
- Reflection about the y-axis
- Reflection about an axis perpendicular to xy plane and passing through the origin
- Reflection about line y=x
1. Reflection about x-axis: The object can be reflected about x-axis with the help of the following matrix
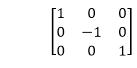
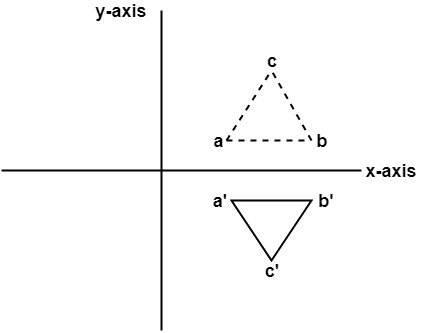
In this transformation value of x will remain same whereas the value of y will become negative. Following figures shows the reflection of the object axis. The object will lie another side of the x-axis.
2. Reflection about y-axis: The object can be reflected about y-axis with the help of following transformation matrix
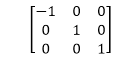
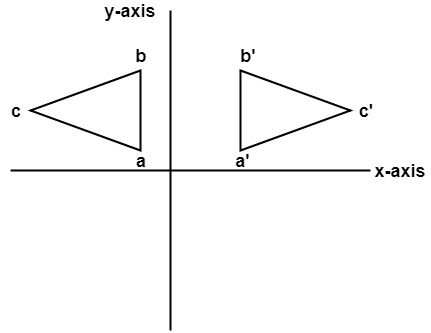
Here the values of x will be reversed, whereas the value of y will remain the same. The object will lie another side of the y-axis.
The following figure shows the reflection about the y-axis
3. Reflection about an axis perpendicular to xy plane and passing through origin:
In the matrix of this transformation is given below
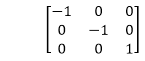
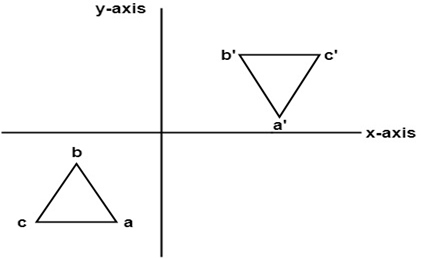
In this value of x and y both will be reversed. This is also called as half revolution about the origin.
4. Reflection about line y=x: The object may be reflected about line y = x with the help of following transformation matrix
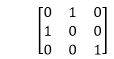
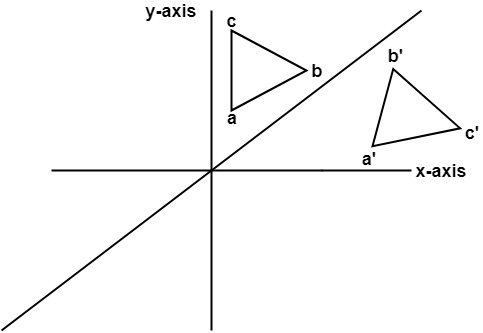
First of all, the object is rotated at 45°. The direction of rotation is clockwise. After it reflection is done concerning x-axis. The last step is the rotation of y=x back to its original position that is counterclockwise at 45°.
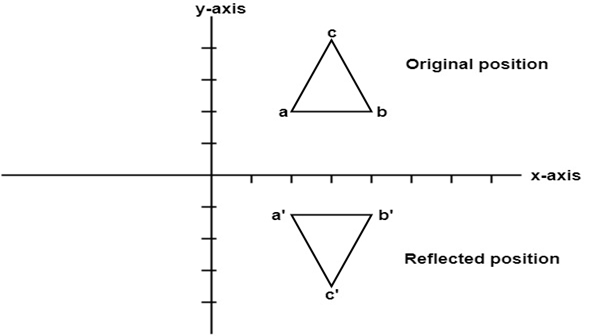
Example: Find reflected position of triangle i.e., to the x-axis.
Solution:

The a point coordinates after reflection
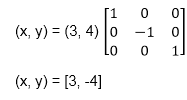
The b point coordinates after reflection
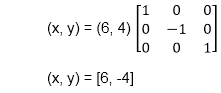
The coordinate of point c after reflection
a (3, 4) becomes a1 (3, -4)
b (6, 4) becomes b1 (6, -4)
c (4, 8) becomes c1 (4, -8)
Shearing:
It is transformation which changes the shape of object. The sliding of layers of object occur. The shear can be in one direction or in two directions.
Shearing in the X-direction:
In this horizontal shearing sliding of layers occur. The homogeneous matrix for shearing in the x-direction is shown below:
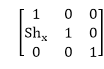
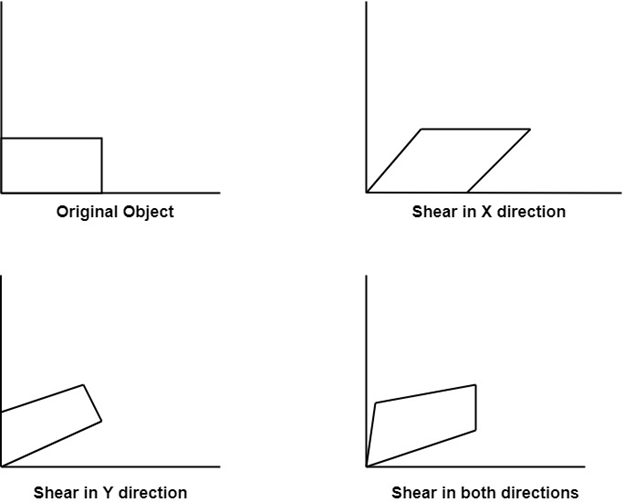
Shearing in the Y-direction: Here shearing is done by sliding along vertical or y-axis.
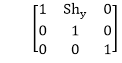
Shearing in X-Y directions:
Here layers will be sided in both x as well as y direction. The sliding will be in horizontal as well as vertical direction. The shape of the object will be distorted. The matrix of shear in both directions is given by:
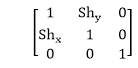
Composite Transformation:
A number of transformations or sequence of transformations can be combined into single one called as composition. The resulting matrix is called as composite matrix. The process of combining is called as concatenation. Suppose we want to perform rotation about an arbitrary point, then we can perform it by the sequence of three transformations
- Translation
- Rotation
- Reverse Translation
The ordering sequence of these numbers of transformations must not be changed. If a matrix is represented in column form, then the composite transformation is performed by multiplying matrix in order from right to left side. The output obtained from the previous matrix is multiplied with the new coming matrix.
Example showing composite transformations:
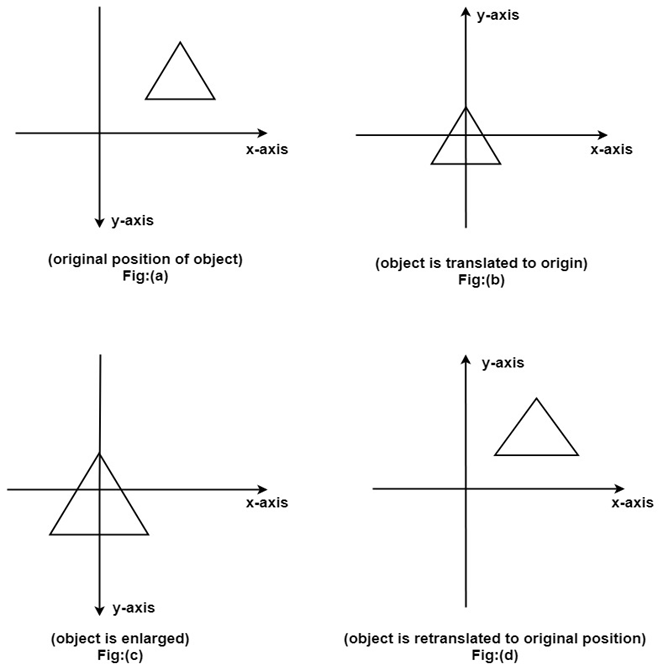
The enlargement is with respect to center. For this following sequence of transformations will be performed and all will be combined to a single one. Composition of two Scaling: The composition of two scaling is multiplicative. Let S11 and S12are matrix to be multiplied.
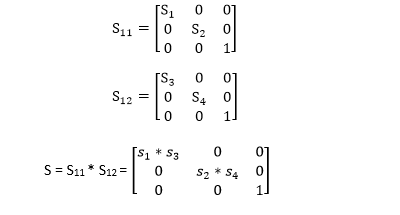
Step1: The object is kept at its position as in fig (a)
Step2: The object is translated so that its center coincides with the origin as in fig (b)
Step3: Scaling of an object by keeping the object at origin is done in fig (c)
Step4: Again translation is done. This second translation is called a reverse translation. It will position the object at the origin location.
Above transformation can be represented as TV.STV-1
Note: Two types of rotations are used for representing matrices one is column method. Another is the row method.

Advantage of composition or concatenation of matrix:
- It transformations become compact.
- The number of operations will be reduced.
- Rules used for defining transformation in form of equations are complex as compared to matrix.
Composition of two translations:
Let t1 t2 t3 t4are translation vectors. They are two translations P1 and P2. The matrix of P1 and P2 given below. The P1 and P2are represented using Homogeneous matrices and P will be the final transformation matrix obtained after multiplication.
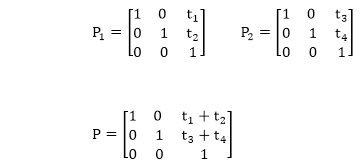
Above resultant matrix show that two successive translations are additive.
Composition of two Rotations: Two Rotations are also additive
Composition of two Scaling: The composition of two scaling is multiplicative. Let S11 and S12are matrix to be multiplied.
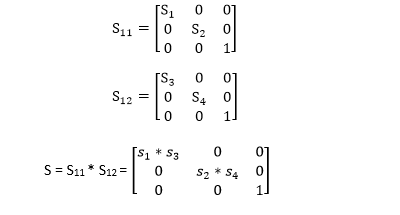

0 Comments