Relational Algebra
- The part of mathematics in which letters and other general symbols are used to represent numbers and quantities in formula and equations.
- Ex: (x + y) · z = (x · z) + (y · z).
- The main application of relational algebra is providing a theoretical foundation for relational databases, particularly query languages for such databases.
- Relational algebra is a formal system for manipulating relations.
- Operands of this algebra are relations.
- Operations of this algebra include the usual set operations (since relations are sets of tuples), and special operations defined for relations
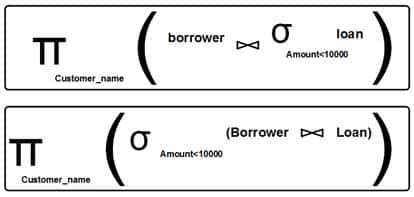
- selection
- projection
- join
The Relational Model
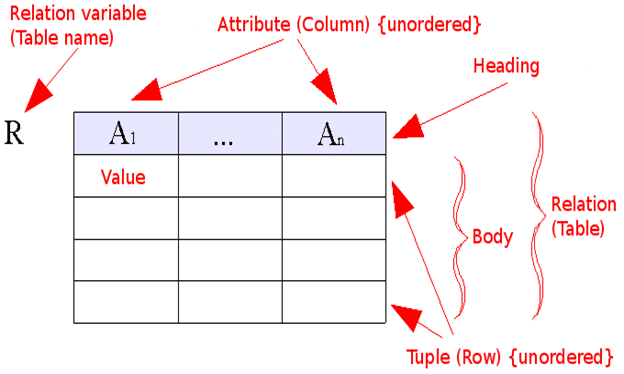
- Data and relationships are represented by a collection of tables.
- Each table has a number of columns with unique names, e.g. customer, account.
Example of a Relation
Attribute Types
- The set of allowed values for each attribute is called the domain of the attribute
- Attribute values are (normally) required to be atomic; that is, indivisible
- The special value null is a member of every domain
- The null value causes complications in the definition of many operations
Relation Schema
- A set of attributes is called a relation schema .
- A1, A2, …, An are attributes
- R = (A1, A2, …, An ) is a relation schema
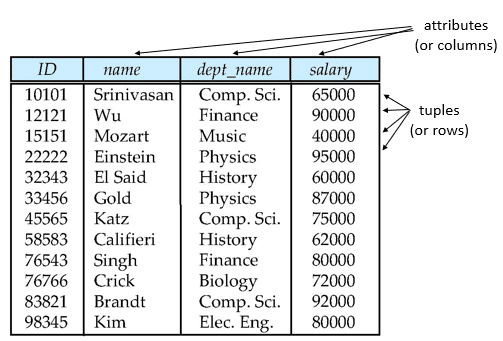
Example:
instructor = (ID, name, dept_name, salary)
Or,
time_slot (time_slot_id , day, start_time , end_time )
- The current values (relation instance) of a relation are specified by a table
- An element t of r is a tuple, represented by a rowin a table
The current values (relation instance) of a relation are specified by a table
An element t of r is a tuple, represented by a rowin a table

0 Comments