Scan Converting a Ellipse:
The ellipse is also a symmetric figure like a circle but is four-way symmetry rather than eight-way.
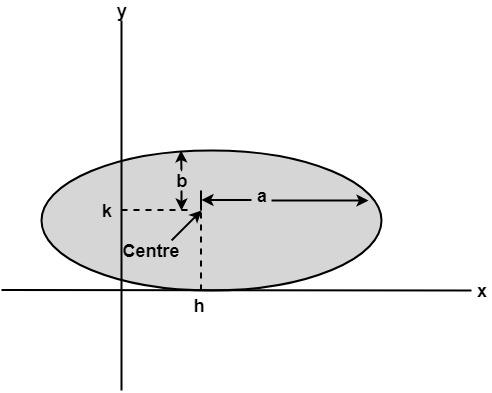
Program to Implement Ellipse Drawing Algorithm:
-
#include<stdio.h> #include<conio.h> #include<graphics.h> #include<math.h> void display(); float x,y; int xc,yc; int main() { int gd=DETECT,gm,a,b; float p1,p2; //clrscr(); initgraph(&gd,&gm,"c:\\turboc3\\bgi"); printf(" Ellipse Generating Algorithm \n\n"); printf("Enter the value of Xc\t"); scanf("%d",&xc); printf("Enter the value of Yc\t"); scanf("%d",&yc); printf("Enter X axis length\t"); scanf("%d",&a); printf("Enter Y axis length\t"); scanf("%d",&b); x=0;y=b; display(); p1=(b*b)-(a*a*b)+(a*a)/4; while((2.0*b*b*x)<=(2.0*a*a*y)) { x++; if(p1<=0) p1=p1+(2.0*b*b*x)+(b*b); else { y--; p1=p1+(2.0*b*b*x)+(b*b)-(2.0*a*a*y); } display(); x=-x; display(); x=-x; delay(50); } x=a; y=0; display(); p2=(a*a)+2.0*(b*b*a)+(b*b)/4; while((2.0*b*b*x)>(2.0*a*a*y)) { y++; if(p2>0) p2=p2+(a*a)-(2.0*a*a*y); else { x--; p2=p2+(2.0*b*b*x)-(2.0*a*a*y)+(a*a); } display(); y=-y; display(); y=-y; delay(50); } getch(); closegraph(); } void display() { putpixel(xc+x,yc+y,7); putpixel(xc-x,yc+y,7); putpixel(xc+x,yc-y,7); putpixel(xc+x,yc-y,7); }Output:
There two methods of defining an Ellipse:
- Polynomial Method of defining an Ellipse
- Trigonometric method of defining an Ellipse
Polynomial Method:
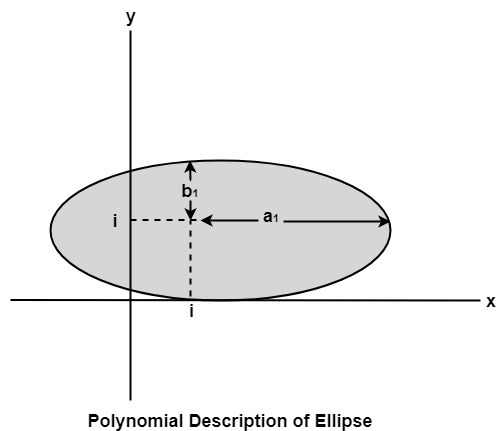
The ellipse has a major and minor axis. If a1 and b1are major and minor axis respectively. The centre of ellipse is (i, j). The value of x will be incremented from i to a1and value of y will be calculated using the following formula
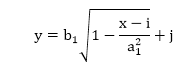
Drawback of Polynomial Method:
- It requires squaring of values. So floating point calculation is required.
- Routines developed for such calculations are very complex and slow.
Algorithm:
1. Set the initial variables: a = length of major axis; b = length of minor axis; (h, k) = coordinates of ellipse center; x = 0; i = step; xend = a.
2. Test to determine whether the entire ellipse has been scan-converted. If x>xend, stop.
3. Compute the value of the y coordinate:
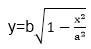
4. Plot the four points, found by symmetry, at the current (x, y) coordinates:
Plot (x + h, y + k) Plot (-x + h, -y + k) Plot (-y – h, x + k) Plot (y + h, -x + k)
5. Increment x; x = x + i.
6. Go to step 2.
Program to draw an Ellipse using Polynomial Method:
#include <graphics.h>
#include <stdlib.h>
#include <math.h>
#include <stdio.h>
#include <conio.h>
#include <iostream>
using namespace std;
class bresen
{
float x, y, a, b, r, t, te, xend, h, k, step;
public:
void get ();
void cal ();
};
int main ()
{
bresen b;
b.get ();
b.cal ();
getch ();
}
void bresen :: get ()
{
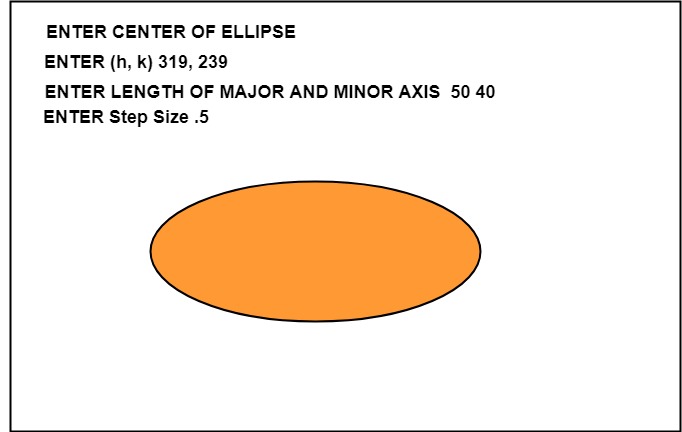
cout<<"\n ENTER CENTER OF ELLIPSE";
cout<<"\n enter (h, k) ";
cin>>h>>k;
cout<<"\n ENTER LENGTH OF MAJOR AND MINOR AXIS";
cin>>a>>b;
cout<<"\n ENTER Step Size";
cin>> step;
}
void bresen ::cal ()
{
/* request auto detection */
int gdriver = DETECT,gmode, errorcode;
int midx, midy, i;
/* initialize graphics and local variables */
initgraph (&gdriver, &gmode, " ");
/* read result of initialization */
errorcode = graphresult ();
if (errorcode != grOk) /* an error occurred */
{
printf("Graphics error: %s\n", grapherrormsg(errorcode));
printf("Press any key to halt:");
getch();
exit(1); /* terminate with an error code */
}
x = 0;
xend=a;
while (x<xend)
{
t= (1-((x * x)/ (a * a)));
if (t<0)
te=-t;
else
te=t;
y=b * sqrt (te);
putpixel (h+x, k+y, RED);
putpixel (h-x, k+y, RED);
putpixel (h+x, y-y, RED);
putpixel (h-x, k-y, RED);
x+=step;
}
getch();
}
Output:
Trignometric Method:
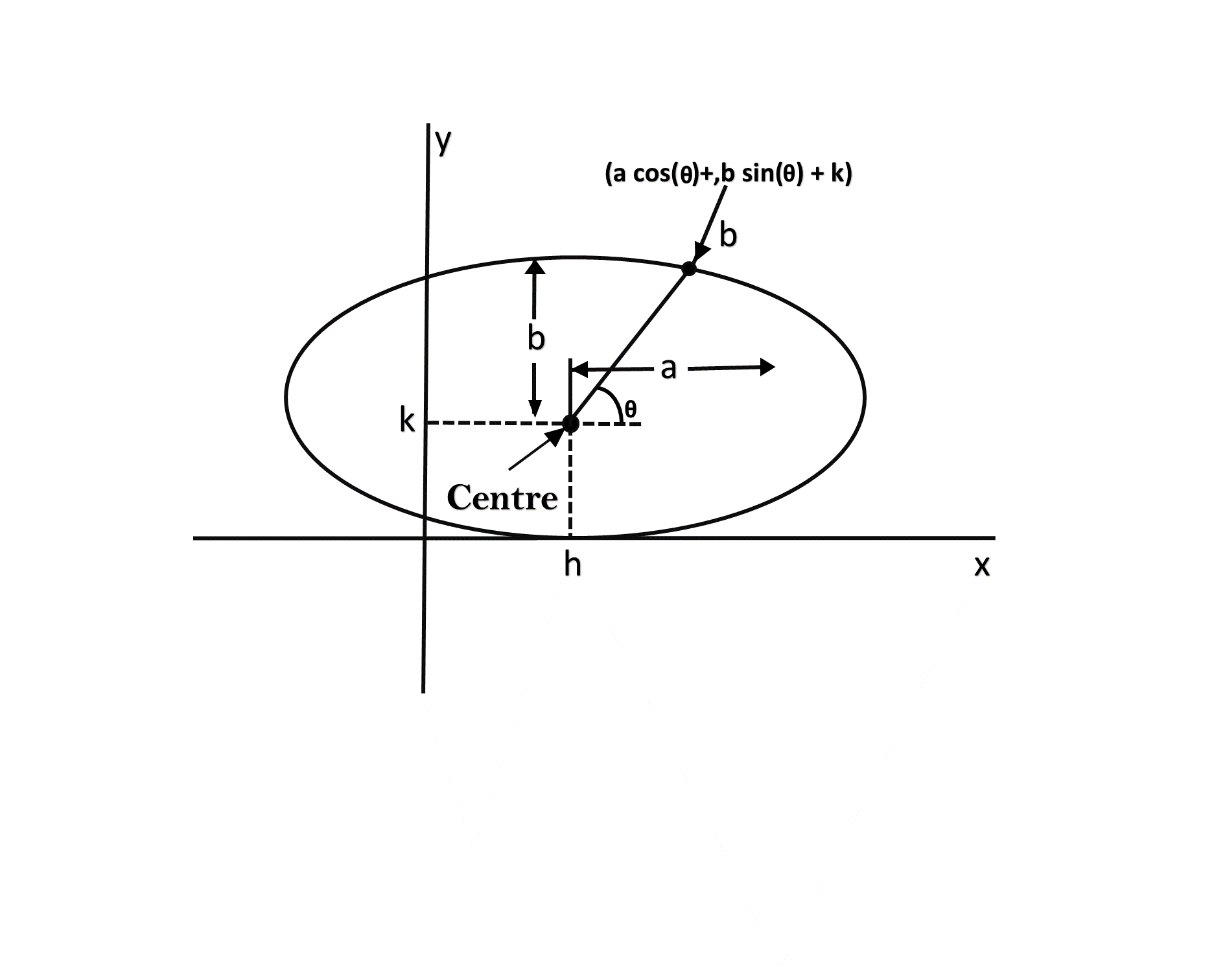
The following equation defines an ellipse trigonometrically as shown in fig:
x = a * cos (θ) +h and
y = b * sin (θ)+k
where (x, y) = the current coordinates
a = length of major axis
b = length of minor axis
θ= current angle
(h, k) = ellipse center
In this method, the value of θ is varied from 0 to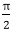 
radians. The remaining points are found by symmetry.
Drawback:
- This is an inefficient method.
- It is not an interactive method for generating ellipse.
- The table is required to see the trigonometric value.
- Memory is required to store the value of θ.
Algorithm:
Step1: Start Algorithm
Step2: Declare variable x1,y1,aa1,bb1,aa2,bb2,fx,fy,p1,a1,b1
Step3: Initialize x1=0 and y1=b/* values of starting point of circle */
Step4: Calculate aa1=a1*a1
Calculate bb1=b1* b1
Calculate aa2=aa1*2
Calculate bb2=bb1*2
Step5: Initialize fx = 0
Step6: Initialize fy = aa_2* b1
Step7: Calculate the value of p1and round if it is integer
p1=bb1-aa1* b1+0.25* aa1/
Step8:
While (fx < fy)
{
Set pixel (x1,y1)
Increment x i.e., x = x + 1
Calculate fx = fx + bb2
If (p1 < 0)
Calculate p1 = p1 + fx + bb1/
else
{
Decrement y i.e., y = y-1
Calculate fy = fy - 992;
p1=p1 + fx + bb1-fy
}
}
Step9: Setpixel (x1,y1)
Step10: Calculate p1=bb1 (x+.5)(x+.5)+aa(y-1)(y-1)-aa1*bb1
Step 11:
While (y1>0)
{
Decrement y i.e., y = y-1
fy=fx-aa2/
if (p1>=0)
p1=p1 - fx + aa1/
else
{
Increment x i.e., x = x + 1
fx= fx+bb_2
p1=p1+fx-fy-aa1
}
}
Set pixel (x1,y1)
Step12: Stop Algorithm
Program to draw a circle using Trigonometric method:
#include <graphics.h>
#include <stdlib.h>
#include <math.h>
#include <stdio.h>
#include <conio.h>
#include <iostream>
# define pi 3.14
using namespace std;
class bresen
{
float a, b, h, k, thetaend,step,x,y;
int i;
public:
void get ();
void cal ();
};
int main ()
{
bresen b;
b.get ();
b.cal ();
getch ();
}
void bresen :: get ()
{
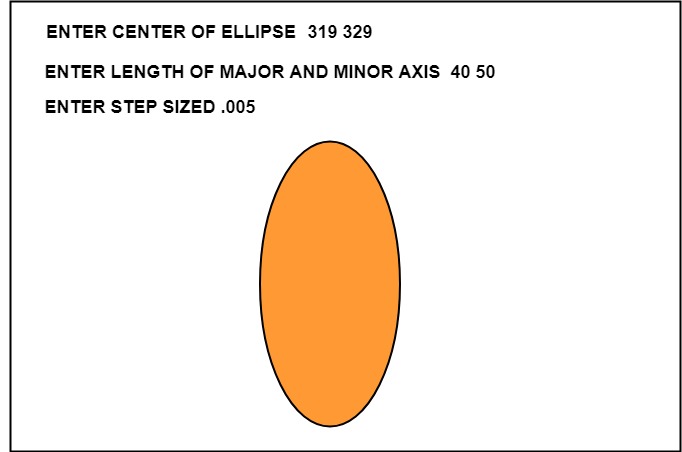
cout<<"\n ENTER CENTER OF ELLIPSE";
cin>>h>>k;
cout<<"\n ENTER LENGTH OF MAJOR AND MINOR AXIS";
cin>>a>>b;
cout<<"\n ENTER STEP SIZE";
cin>> step;
}
void bresen ::cal ()
{
/* request auto detection */
int gdriver = DETECT,gmode, errorcode;
int midx, midy, i;
/* initialize graphics and local variables */
initgraph (&gdriver, &gmode, " ");
/* read result of initialization */
errorcode = graphresult ();
if (errorcode != grOk) /* an error occurred */
{
printf("Graphics error: %s\n", grapherrormsg(errorcode));
printf("Press any key to halt:");
getch();
exit(1); /* terminate with an error code */
}
int theta = 0;
thetaend=(pi*90)/180;
while (theta<thetaend)
{
x = a * cos (theta);
y = b * sin (theta);
putpixel (x+h, y+k, RED);
putpixel (-x+h, y+k, RED);
putpixel (-x+h, -y+k, RED);
putpixel (x+h, -y+k, RED);
theta+=step;
}
getch();
}
Output:
Ellipse Axis Rotation:
Since the ellipse shows four-way symmetry, it can easily be rotated. The new equation is found by trading a and b, the values which describe the major and minor axes. When the polynomial method is used, the equations used to describe the ellipse become
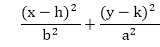
where (h, k) = ellipse center
a = length of the major axis
b = length of the minor axis
In the trigonometric method, the equations are
x = b cos (θ)+h and y=a sin(θ)+k
Where (x, y) = current coordinates
a = length of the major axis
b = length of the minor axis
θ = current angle
(h, k) = ellipse center
Assume that you would like to rotate the ellipse through an angle other than 90 degrees. The rotation of the ellipse may be accomplished by rotating the x &y axis α degrees.
x = a cos (0) – b sin (0+ ∞) + h y= b (sin 0) + a cos (0+∞) + k
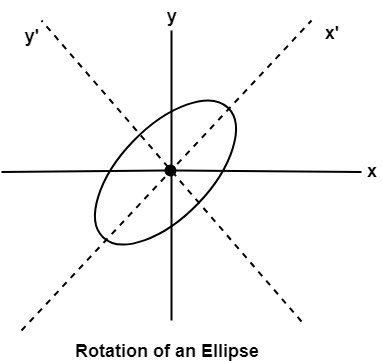
Midpoint Ellipse Algorithm:
This is an incremental method for scan converting an ellipse that is centered at the origin in standard position i.e., with the major and minor axis parallel to coordinate system axis. It is very similar to the midpoint circle algorithm. Because of the four-way symmetry property we need to consider the entire elliptical curve in the first quadrant.
Let’s first rewrite the ellipse equation and define the function f that can be used to decide if the midpoint between two candidate pixels is inside or outside the ellipse:
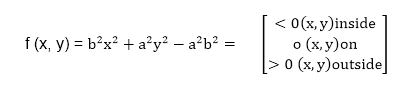
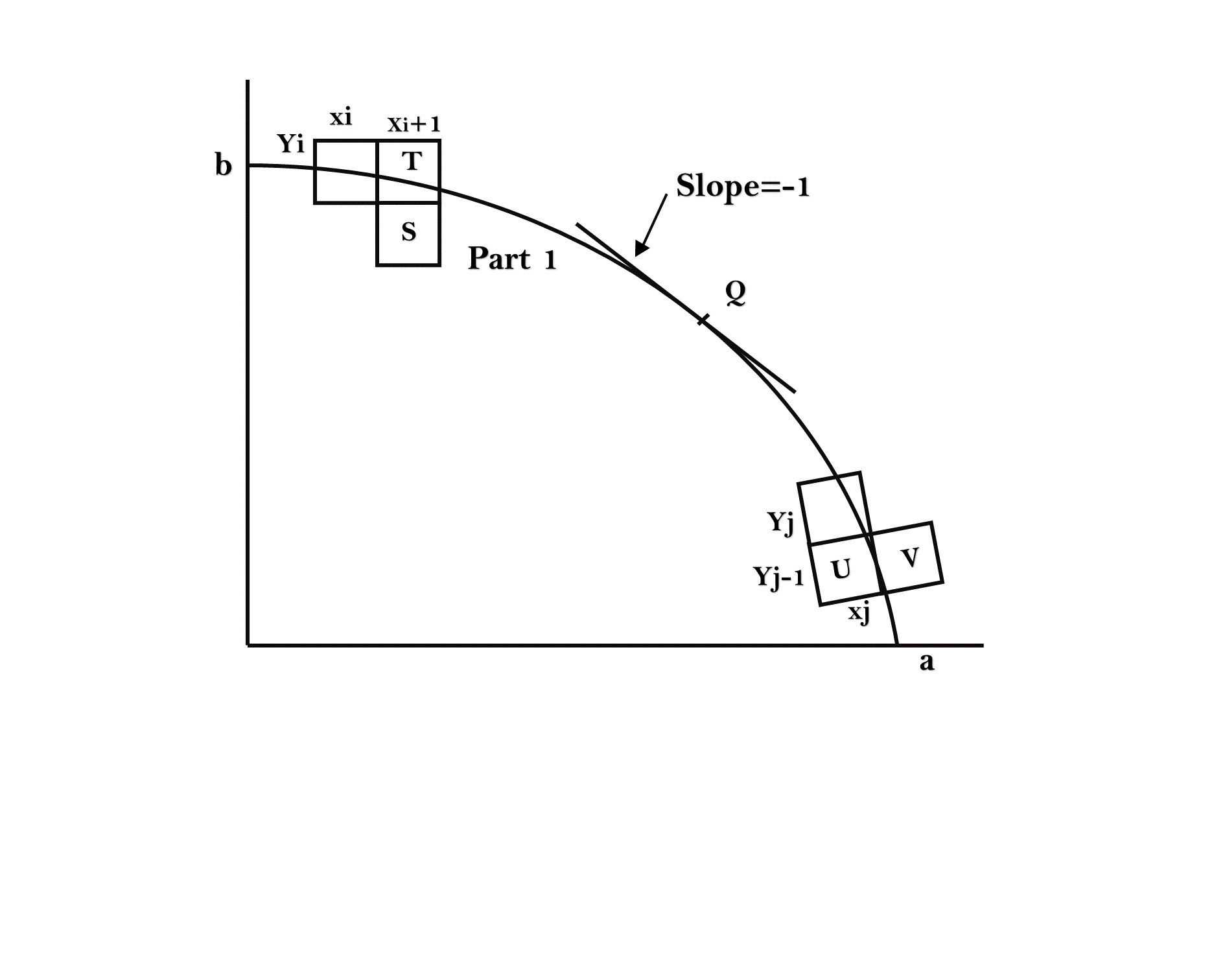
Now divide the elliptical curve from (0, b) to (a, 0) into two parts at point Q where the slope of the curve is -1.
Slope of the curve is defined by the f(x, y) = 0 is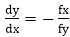
where fx & fy are partial derivatives of f(x, y) with respect to x & y.
We have fx = 2b2 x, fy=2a2 y &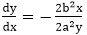 
Hence we can monitor the slope value during the scan conversion process to detect Q. Our starting point is (0, b)
Suppose that the coordinates of the last scan converted pixel upon entering step i are (xi,yi). We are to select either T (xi+1),yi) or S (xi+1,yi-1) to be the next pixel. The midpoint of T & S is used to define the following decision parameter.
pi = f(xi+1),yi–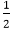
)
pi=b2 (xi+1)2+a2 (yi–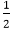)2-a2 b2
If pi<0, the midpoint is inside the curve and we choose pixel T.
If pi>0, the midpoint is outside or on the curve and we choose pixel S.
Decision parameter for the next step is:
pi+1=f(xi+1+1,yi+1–)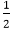
= b2 (xi+1+1)2+a2 (yi+1–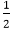)2-a2 b2
Since xi+1=xi+1,we have
pi+1-pi=b2[((xi+1+1)2+a2 (yi+1–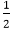)2-(yi –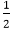)2]
pi+1= pi+2b2 xi+1+b2+a2 [(yi+1–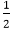)2-(yi –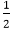)2]
If T is chosen pixel (pi<0), we have yi+1=yi.
If S is chosen pixel (pi>0) we have yi+1=yi-1. Thus we can express
pi+1in terms of pi and (xi+1,yi+1): pi+1= pi+2b2 xi+1+b2 if pi<0 = pi+2b2 xi+1+b2-2a2 yi+1 if pi>0
The initial value for the recursive expression can be obtained by the evaluating the original definition of pi with (0, b):
p1 = (b2+a2 (b-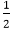)2-a2 b2
= b2-a2 b+a2/4
Suppose the pixel (xj yj) has just been scan converted upon entering step j. The next pixel is either U (xj ,yj-1) or V (xj+1,yj-1). The midpoint of the horizontal line connecting U & V is used to define the decision parameter:
qj=f(xj+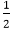,yj-1)
qj=b2 (xj+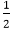)2+a2 (yj -1)2-a2 b2
If qj<0, the midpoint is inside the curve and we choose pixel V.
If qj≥0, the midpoint is outside the curve and we choose pixel U.Decision parameter for the next step is:
qj+1=f(xj+1+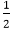,yj+1-1)
= b2 (xj+1+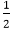)2+ a2 (yj+1-1)2– a2 b2
Since yj+1=yj-1,we have
qj+1-qj=b2 [(xj+1+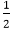)2-(xj +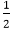)2 ]+a2 (yj+1-1)2-( yj+1)2 ]
qj+1=qj+b2 [(xj+1+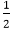)2-(xj +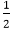)2]-2a2 yj+1+a2
If V is chosen pixel (qj<0), we have xj+1=xj.
If U is chosen pixel (pi>0) we have xj+1=xj. Thus we can express
qj+1in terms of qj and (xj+1,yj+1 ):
qj+1=qj+2b2 xj+1-2a2 yj+1+a2 if qj < 0
=qj-2a2 yj+1+a2 if qj>0
The initial value for the recursive expression is computed using the original definition of qj. And the coordinates of (xk yk) of the last pixel choosen for the part 1 of the curve:
q1 = f(xk+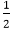,yk-1)=b2 (xk+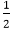)2-a2 (yk-1)2– a2 b2
Algorithm:
int x=0, y=b; [starting point]
int fx=0, fy=2a2 b [initial partial derivatives]
int p = b2-a2 b+a2/4
while (fx2;
if (p<0)
p = p + fx +b2;
else
{
y--;
fy=fy-2a2
p = p + fx +b2-fy;
}
}
Setpixel (x, y);
p=b2(x+0.5)2+ a2 (y-1)2- a2 b2
while (y>0)
{
y--;
fy=fy-2a2;
if (p>=0)
p=p-fy+a2
else
{
x++;
fx=fx+2b2
p=p+fx-fy+a2;
}
Setpixel (x,y);
}
Program to draw an ellipse using Midpoint Ellipse Algorithm:
