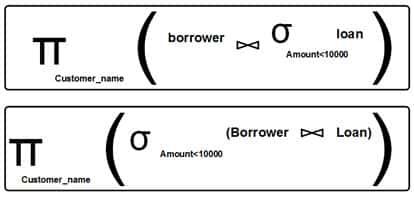
Relational Algebra

• The part of mathematics in which letters and other general symbols are used to represent numbers and quantities in formula and equations.
• Ex: (x + y) · z = (x · z) + (y · z).
• The main application of relational algebra is providing a theoretical foundation for relational databases, particularly query languages for such databases.
• Relational algebra is a formal system for manipulating relations.
• Operands of this algebra are relations.
• Operations of this algebra include the usual set operations (since relations are sets of tuples), and special operations defined for relations
  • selection
  • projection
  • join

The Relational Model

• Data and relationships are represented by a collection of tables.
• Each table has a number of columns with unique names, e.g. customer, account.

Example of a Relation

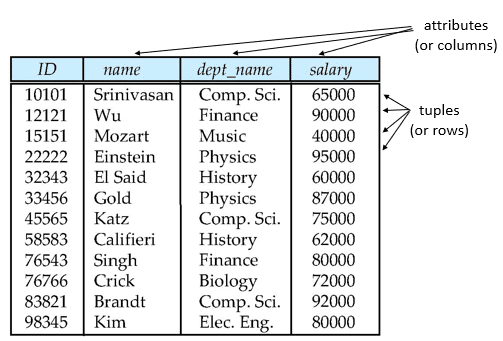
Attribute Types

• The set of allowed values for each attribute is called the domain of the attribute
• Attribute values are (normally) required to be atomic; that is, indivisible
• The special value null  is a member of every domain
• The null value causes complications in the definition of many operations

Relation Schema

• A set of attributes is called a relation schema .
• A₁, A₂, …, A_n are attributes
• R = (A₁, A₂, …, A_n ) is a relation schema

            Example:

                 instructor  = (ID,  name, dept_name, salary)

Or,

    time_slot (time_slot_id , day, start_time , end_time )

• The current values (relation instance) of a relation are specified by a table
• An element t of r is a tuple, represented by a rowin a table

The current values (relation instance) of a relation are specified by a table

An element t of r is a tuple, represented by a rowin a table